Solución a la tarea 6
Programación y métodos estadísticos avanzados en
R
Marcelo
Araya-Salas, PhD
“2022-10-31”
Los conceptos error tipo I y error tipo II nos permiten entender la robustez (o fragilidad) de nuestras herramientas estádisticas:
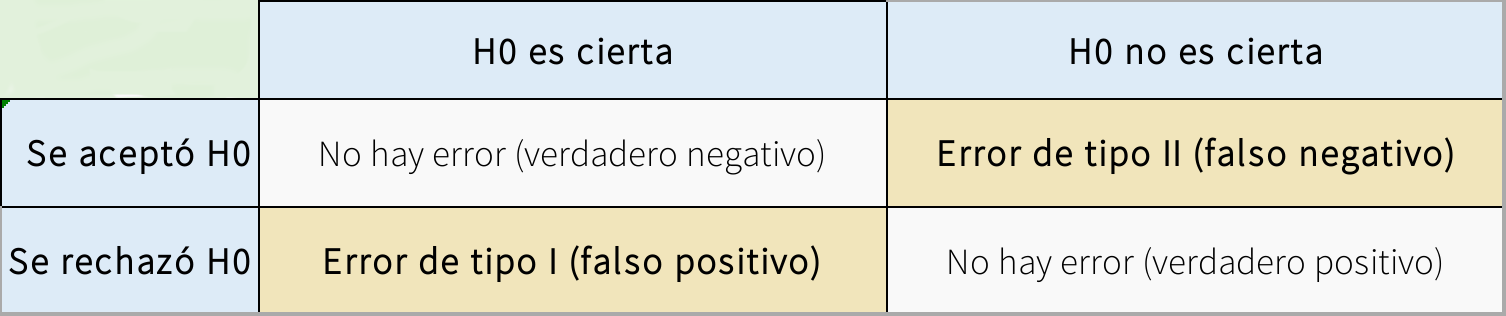
Estos conceptos se suelen cuantificar con 2 medidas relacionadas: el poder estadístico y la tasa de error tipo I. El poder estadístico es la probabilidad de que una prueba rechace (correctamente) una hipótesis nula falsa. Osea la probabilidad de encontrar una diferencia significativa cuando si la hay. La tasa de error tipo I se refiere a la probabilidad de encontrar una diferencia significativa cuando no la hay. En esta tarea exploraremos estos conceptos combinando bucles con simulaciones estadísticas.
Primero vamos a definir las simulaciones que usaremos. El siguiente código simula un juego de datos donde el predictor y la variable respuesta no están asociados:
# definir semilla
set.seed(123)
# numero de observaciones
n <- 50
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
y <- rnorm(n = n, mean = 0, sd = 1)
# crear data frame
xy_datos <- data.frame(x1, y)Podemos correr un modelo lineal que estime la (falta de) asociación entre las variables:
# construir model
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
# calcular el resumen
summ <- summary(xy_mod)
# extraer el valor de p
summ$coefficients[2, 4]## [1] 0.805Note que la última linea de código devuelve el valor de p.
También podemos hacer el mismo ejercicio con un juego de datos donde las variables están asociadas de la siguiente forma:
# numero de observaciones
n <- 50
b0 <- -4
b1 <- 0.55
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
error <- rnorm(n = n, mean = 0, sd = 1)
y <- b0 + b1 * x1 + error
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
# extraer el valor de p
summ$coefficients[2, 4]## [1] 0.000221- Haga un bucle
replicateque repita la simulación de variables no asociadas 1000 veces y que calcule el valor de p para cada juego de datos simulado en cada iteración. ¿Qué proporción de las 1000 repeticiones produjo un valor de p mayor o igual a 0.05 (osea, no fueron significativos)? Note que estamos calculando la tasa de error tipo I.
# numero de observaciones
n <- 30
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
y <- rnorm(n = n, mean = 0, sd = 1)
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.95
- Corra el bucle anterior pero esta vez haga que la simulación genere
solo 5 observaciones por replica (en vez de las 30 observaciones, pista:
n <- 5). ¿Como afecta este cambio la proporción de repeticiones con un valor de p mayor o igual a 0.05?
# numero de observaciones
n <- 5
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
y <- rnorm(n = n, mean = 0, sd = 1)
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.96
- Haga un bucle
replicateque repita la simulación de variables asociadas 1000 veces y que calcule el valor de p para cada juego de datos simulado en cada iteración. ¿Qué proporción de las 1000 repeticiones produjo un valor de p mayor o igual a 0.05? Note que esta es una medida del poder estadístico.
# numero de observaciones
n <- 50
b0 <- -4
b1 <- 0.55
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
error <- rnorm(n = n, mean = 0, sd = 1)
y <- b0 + b1 * x1 + error
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.035
- Corra el bucle anterior pero esta vez haga que la simulación genere
solo 5 observaciones por replica (en vez de las 30 observaciones, pista:
n = 5). ¿Como afecta este cambio la proporción de repeticiones con un valor de p mayor o igual a 0.05?
# numero de observaciones
n <- 5
b0 <- -4
b1 <- 0.55
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rnorm(n = n, mean = 0, sd = 1)
y <- b0 + b1 * x1 + rnorm(n)
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.874
- Corra de nuevo el bucle del punto 1 (variables no asociadas) pero
esta vez use la función
rbinom()para generar ‘x1’ (puede usarrbinom(n = n, size = 4, prob = 0.6)para esto). ¿Como afecta este cambio la proporción de repeticiones con un valor de p mayor o igual a 0.05?
# numero de observaciones
n <- 30
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rbinom(n = n, size = 4, prob = 0.6)
y <- rnorm(n = n, mean = 0, sd = 1)
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.949
- Corra de nuevo el bucle del punto 2 (variables asociadas) pero esta
vez use la función
rbinom()para generar ‘x1’ (puede usarrbinom(n = n, size = 4, prob = 0.6)para esto). ¿Como afecta este cambio la proporción de repeticiones con un valor de p mayor o igual a 0.05?
# numero de observaciones
n <- 30
b0 <- -4
b1 <- 0.55
reps <- replicate(n = 1000, expr = {
# variables aleatorias
x1 <- rbinom(n = n, size = 4, prob = 0.6)
y <- b0 + b1 * x1 + rnorm(n)
# crear data frame
xy_datos <- data.frame(x1, y)
xy_mod <- lm(formula = y ~ x1, data = xy_datos)
summ <- summary(xy_mod)
pval <- summ$coefficients[2, 4]
return(pval)
})
sum(reps > 0.05)/length(reps)## [1] 0.235
Información de la sesión
## R version 4.1.1 (2021-08-10)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 20.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
##
## locale:
## [1] LC_CTYPE=es_ES.UTF-8
## [2] LC_NUMERIC=C
## [3] LC_TIME=es_CR.UTF-8
## [4] LC_COLLATE=es_ES.UTF-8
## [5] LC_MONETARY=es_CR.UTF-8
## [6] LC_MESSAGES=es_ES.UTF-8
## [7] LC_PAPER=es_CR.UTF-8
## [8] LC_NAME=C
## [9] LC_ADDRESS=C
## [10] LC_TELEPHONE=C
## [11] LC_MEASUREMENT=es_CR.UTF-8
## [12] LC_IDENTIFICATION=C
##
## attached base packages:
## [1] stats graphics grDevices utils datasets
## [6] methods base
##
## other attached packages:
## [1] DT_0.23 tufte_0.12
## [3] rticles_0.24 revealjs_0.9
## [5] rmdformats_1.0.4 rmarkdown_2.14
## [7] sketchy_1.0.2 remotes_2.4.2
## [9] leaflet_2.1.1 car_3.1-0
## [11] carData_3.0-5 sjPlot_2.8.10
## [13] lmerTest_3.1-3 lme4_1.1-29
## [15] Matrix_1.3-4 scales_1.2.0
## [17] MASS_7.3-54 emo_0.0.0.9000
## [19] viridis_0.6.2 viridisLite_0.4.0
## [21] xaringanExtra_0.7.0 ggplot2_3.3.6
## [23] RColorBrewer_1.1-3 kableExtra_1.3.4
## [25] knitr_1.39
##
## loaded via a namespace (and not attached):
## [1] minqa_1.2.4 colorspace_2.0-3
## [3] ellipsis_0.3.2 rsconnect_0.8.26
## [5] sjlabelled_1.2.0 rprojroot_2.0.3
## [7] estimability_1.3 parameters_0.18.1
## [9] fs_1.5.2 rstudioapi_0.13
## [11] farver_2.1.1 fansi_1.0.3
## [13] mvtnorm_1.1-3 lubridate_1.8.0
## [15] xml2_1.3.3 splines_4.1.1
## [17] cachem_1.0.6 sjmisc_2.8.9
## [19] pkgload_1.2.4 jsonlite_1.8.0
## [21] nloptr_2.0.3 ggeffects_1.1.2
## [23] packrat_0.8.0 broom_0.8.0
## [25] effectsize_0.7.0 compiler_4.1.1
## [27] httr_1.4.3 backports_1.4.1
## [29] sjstats_0.18.1 emmeans_1.7.4-1
## [31] assertthat_0.2.1 fastmap_1.1.0
## [33] cli_3.3.0 formatR_1.12
## [35] htmltools_0.5.3 prettyunits_1.1.1
## [37] tools_4.1.1 coda_0.19-4
## [39] gtable_0.3.0 glue_1.6.2
## [41] dplyr_1.0.9 Rcpp_1.0.9
## [43] jquerylib_0.1.4 vctrs_0.4.1
## [45] svglite_2.1.0 nlme_3.1-152
## [47] crosstalk_1.2.0 insight_0.17.1
## [49] xfun_0.31 stringr_1.4.0
## [51] ps_1.7.1 brio_1.1.3
## [53] testthat_3.1.4 rvest_1.0.2
## [55] lifecycle_1.0.1 devtools_2.4.3
## [57] ragg_1.2.2 yaml_2.3.5
## [59] memoise_2.0.1 gridExtra_2.3
## [61] sass_0.4.1 stringi_1.7.8
## [63] highr_0.9 bayestestR_0.12.1
## [65] desc_1.4.1 boot_1.3-28
## [67] pkgbuild_1.3.1 rlang_1.0.4
## [69] pkgconfig_2.0.3 systemfonts_1.0.4
## [71] evaluate_0.15 lattice_0.20-44
## [73] purrr_0.3.4 htmlwidgets_1.5.4
## [75] labeling_0.4.2 processx_3.6.1
## [77] tidyselect_1.1.2 bookdown_0.27
## [79] magrittr_2.0.3 R6_2.5.1
## [81] generics_0.1.2 DBI_1.1.3
## [83] pillar_1.8.0 withr_2.5.0
## [85] mgcv_1.8-36 abind_1.4-5
## [87] datawizard_0.4.1 tibble_3.1.8
## [89] performance_0.9.0 modelr_0.1.8
## [91] crayon_1.5.1 uuid_1.1-0
## [93] utf8_1.2.2 usethis_2.1.6
## [95] grid_4.1.1 isoband_0.2.5
## [97] callr_3.7.0 digest_0.6.29
## [99] webshot_0.5.3 xtable_1.8-4
## [101] tidyr_1.2.0 numDeriv_2016.8-1.1
## [103] textshaping_0.3.6 munsell_0.5.0
## [105] bslib_0.3.1 sessioninfo_1.2.2